Difference between revisions of "Response Curve"
m (Added behavior reference) |
m (→Curve Types) |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{IAUS Header}} | {{IAUS Header}} | ||
<hr> | |||
{{Part of Behavior}} | |||
== Concept == | == Concept == | ||
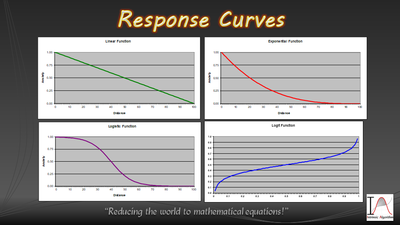
[[File:Response Curves.png|400px|thumb|right|Different types of response curves]] | [[File:Response Curves.png|400px|thumb|right|Different types of response curves]] | ||
| Line 7: | Line 9: | ||
The Response Curve is comprised of a curve type and 4 variables. By changing these values, we change the "shape" of the curve and, therefore, how it converts the raw number into a meaningful value for our utility. | The Response Curve is comprised of a curve type and 4 variables. By changing these values, we change the "shape" of the curve and, therefore, how it converts the raw number into a meaningful value for our utility. | ||
=== Curve | === Curve Type === | ||
The curve types are: | The curve types are: | ||
* Linear | * Linear | ||
Latest revision as of 15:20, 6 October 2021
This page is part of the IAUS Manual. ♦ Brain ♦ Behavior ♦ Behavior Type ♦ Decision ♦ AI Entity ♦
This item is a component of a Behavior.
Concept
A Response Curve is a mathematical formula that converts an input value into an output value. It is a component of a Behavior so that a Behavior can be scored as to its utility for execution.
Components
The Response Curve is comprised of a curve type and 4 variables. By changing these values, we change the "shape" of the curve and, therefore, how it converts the raw number into a meaningful value for our utility.
Curve Type
The curve types are:
- Linear
- Polynomial
- Logistic
- Logit
- Normal (for a normal distribution)
- Sine
Variables
The 4 variables are, m, k, b, and c change their meanings slightly depending on the curve type.
For Linear and Polynomial types, they represent what we are used to seeing in the y = mx + b formula:
- m = slope (positive numbers for up, negative for down)
- k = exponent (1 = linear)
- b = y-intercept
- c = x-intercept
For Logistic curves, they are:
- m = slope of line in middle
- k = Vertical size and direction of curve (positive numbers for up, negative for down)
- b = moves line vertically from its starting point
- c = moves line horizontally from its starting point
For Normal curves, they are:
- m = width of the "bump" of the curve. Roughly equivalent to changing the standard deviation.
- k = height of the "bump"
- b = moves line vertically from its starting point
- c = moves line horizontally from its starting point
Code
The data is held in the very simple ResponseCurve class but the calculations are performed in the Consideration class in Consideration::GetConsiderationValue.